制御系各要素の表現(微分方程式)
制御工学ではブロック線図に登場した各ブロックを数学的に表現します。
数学的に表現することにより ①シミュレーションが可能になる ② 他者との共通認識を得られるといったメリットがあります。
いろいろな数学的表現が存在しますが、まずは微分方程式による表現をしてみます。その後、より便利な伝達関数による表現を行います。
入力と出力
ブロック線図に登場した各要素は、ある値を加えるとそれに対応した値が出てきます。この時、ブロックに加える値のことを入力と呼び、ブロックから出力される値のことを出力と呼びます。
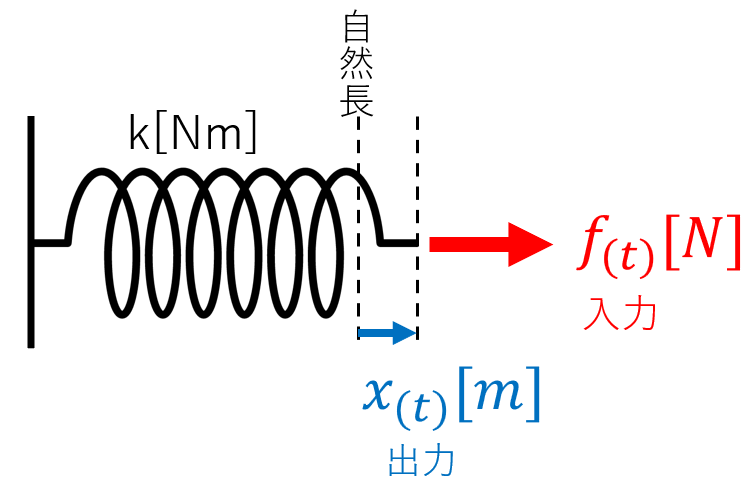
例1 バネ系
下図のようなバネ系を数学的に表現してみましょう。
・バネ定数はk[N/m]
・質量は無視
・入力はバネに加える力f(t)[N]
・出力はバネの伸びx(t)[m]
入出力の関係はフックの法則より
$$f(t)=kx(t)$$
なので、出力を左辺、入力を右辺に移項すると
$$x(t)=\frac{1}{k}f(t)$$
と入力と出力の関係を数式で表すことができました。
例2 マス-バネ-ダンパ系
次は下図のようなマスバネダンパ系を数学的に表現してみましょう。
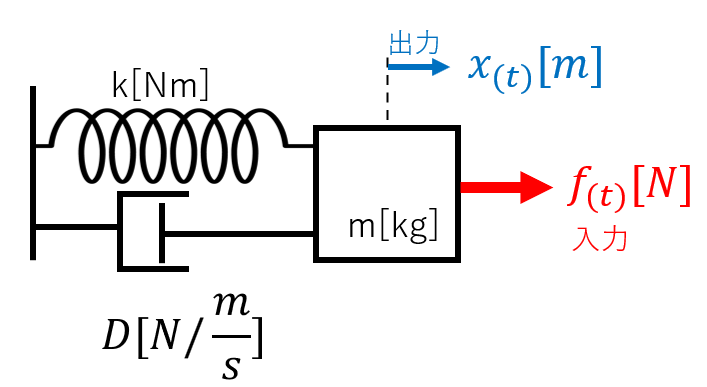
・入力は物体に与える力f(t)[N]
・出力は物体の変位x(t)[m]
・物体の質量m[kg]
・バネ定数k[Nm]
・ダンパ粘性係数D[N/(m/s)]
ニュートンの運動法則より下記式が成り立ちます。

右辺に入力を、左辺に出力を移項すると、下記のように入力と出力の関係を数式で表すことができました。
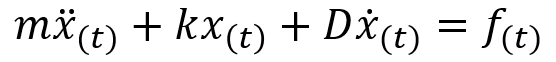
例3 RC回路
次に下図のようなRC回路を表現します。
RC回路とは、電源に加え、名前の通り抵抗R(Resistance)とコンデンサC(Capacitor)で構成される回路です。入力を電源電圧、出力をコンデンサ電圧とします。

変数定義
Vin[V]: 電源電圧
R[Ω]: 抵抗値
C[F]: コンデンサ静電容量
I[A]: 回路に流れる電流
Vout[V]: コンデンサ電圧
電流は単位時間当たりの電荷の変化なので式1がなりたちます。
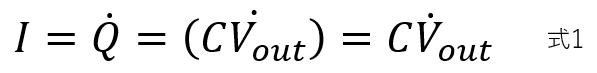
また、キルヒホッフの法則により式2がなりたちます。
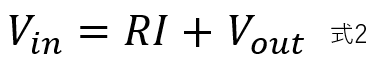
よって、式1を式2に代入することにより下記のように下記のように入力と出力の関係を数式で表すことができました。

